Description:
Given the heads of two singly linked-lists headA and headB, return the node at which the two lists intersect. If the two linked lists have no intersection at all, return null.
For example, the following two linked lists begin to intersect at node c1:
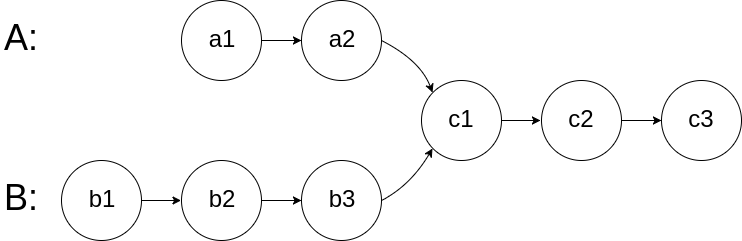
The test cases are generated such that there are no cycles anywhere in the entire linked structure.
Note that the linked lists must retain their original structure after the function returns.
Custom Judge:
The inputs to the judge are given as follows (your program is not given these inputs):
intersectVal– The value of the node where the intersection occurs. This is0if there is no intersected node.listA– The first linked list.listB– The second linked list.skipA– The number of nodes to skip ahead inlistA(starting from the head) to get to the intersected node.skipB– The number of nodes to skip ahead inlistB(starting from the head) to get to the intersected node.
The judge will then create the linked structure based on these inputs and pass the two heads, headA and headB to your program. If you correctly return the intersected node, then your solution will be accepted.
Examples:
Example 1:
Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
Output: Intersected at '8'
Explanation: The intersected node's value is 8 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as [4,1,8,4,5]. From the head of B, it reads as [5,6,1,8,4,5]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B.
- Note that the intersected node's value is not 1 because the nodes with value 1 in A and B (2nd node in A and 3rd node in B) are different node references. In other words, they point to two different locations in memory, while the nodes with value 8 in A and B (3rd node in A and 4th node in B) point to the same location in memory.
Example 2:
Input: intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
Output: Intersected at '2'
Explanation: The intersected node's value is 2 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as [1,9,1,2,4]. From the head of B, it reads as [3,2,4]. There are 3 nodes before the intersected node in A; There are 1 node before the intersected node in B.Solution in Python:
To solve the problem of finding the intersection node of two singly linked lists, we can use a two-pointer technique. This approach is efficient with a time complexity of O(m + n) and a space complexity of O(1), where m and n are the lengths of the two linked lists.
# Definition for singly-linked list.
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> Optional[ListNode]:
if not headA or not headB:
return None
# Initialize two pointers to the heads of the linked lists
pointerA = headA
pointerB = headB
# Loop until the two pointers meet
while pointerA != pointerB:
# If pointerA reaches the end of its list, reset it to the head of listB
if not pointerA:
pointerA = headB
else:
pointerA = pointerA.next
# If pointerB reaches the end of its list, reset it to the head of listA
if not pointerB:
pointerB = headA
else:
pointerB = pointerB.next
# Either both pointers meet at the intersection node, or both are None
return pointerAExplanation:
- Initialization:
- We initialize two pointers,
pointerAandpointerB, to the heads of the two linked lists,headAandheadBrespectively.
- We initialize two pointers,
- Traverse Both Lists:
- We traverse both linked lists with the two pointers. If a pointer reaches the end of its list, it is reset to the head of the other list. This ensures that both pointers traverse equal lengths when they switch lists, which is crucial for finding the intersection point.
- Finding Intersection:
- If the two lists intersect, the pointers will eventually meet at the intersection node after at most
m + nsteps. - If the two lists do not intersect, both pointers will eventually reach the end (
None) simultaneously, and the loop will terminate without finding an intersection.
- If the two lists intersect, the pointers will eventually meet at the intersection node after at most
- Return Result:
- If the pointers meet at some node, that node is the intersection node.
- If the pointers meet at
None, there is no intersection, and we returnNone.
Solution in Javascript:
/**
* Definition for singly-linked list.
* function ListNode(val) {
* this.val = val;
* this.next = null;
* }
*/
/**
* @param {ListNode} headA
* @param {ListNode} headB
* @return {ListNode}
*/
var getIntersectionNode = function(headA, headB) {
// If either headA or headB is null, there can be no intersection
if (headA === null || headB === null) {
return null;
}
// Initialize two pointers to the heads of the linked lists
let pointerA = headA;
let pointerB = headB;
// Loop until the two pointers meet
while (pointerA !== pointerB) {
// If pointerA reaches the end of its list, reset it to the head of listB
pointerA = (pointerA === null) ? headB : pointerA.next;
// If pointerB reaches the end of its list, reset it to the head of listA
pointerB = (pointerB === null) ? headA : pointerB.next;
}
// Either both pointers meet at the intersection node, or both are null
return pointerA;
};Solution in Java:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
// If either headA or headB is null, there can be no intersection
if (headA == null || headB == null) {
return null;
}
// Initialize two pointers to the heads of the linked lists
ListNode pointerA = headA;
ListNode pointerB = headB;
// Loop until the two pointers meet
while (pointerA != pointerB) {
// If pointerA reaches the end of its list, reset it to the head of listB
pointerA = (pointerA == null) ? headB : pointerA.next;
// If pointerB reaches the end of its list, reset it to the head of listA
pointerB = (pointerB == null) ? headA : pointerB.next;
}
// Either both pointers meet at the intersection node, or both are null
return pointerA;
}
}Solution in C#:
/**
* Definition for singly-linked list.
* public class ListNode {
* public int val;
* public ListNode next;
* public ListNode(int x) { val = x; }
* }
*/
public class Solution {
public ListNode GetIntersectionNode(ListNode headA, ListNode headB) {
// If either headA or headB is null, there can be no intersection
if (headA == null || headB == null) {
return null;
}
// Initialize two pointers to the heads of the linked lists
ListNode pointerA = headA;
ListNode pointerB = headB;
// Loop until the two pointers meet
while (pointerA != pointerB) {
// If pointerA reaches the end of its list, reset it to the head of listB
pointerA = (pointerA == null) ? headB : pointerA.next;
// If pointerB reaches the end of its list, reset it to the head of listA
pointerB = (pointerB == null) ? headA : pointerB.next;
}
// Either both pointers meet at the intersection node, or both are null
return pointerA;
}
}