Description
One way to serialize a binary tree is to use preorder traversal. When we encounter a non-null node, we record the node’s value. If it is a null node, we record using a sentinel value such as '#'.
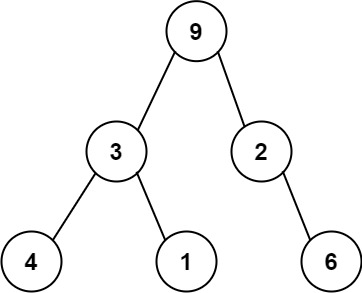
For example, the above binary tree can be serialized to the string "9,3,4,#,#,1,#,#,2,#,6,#,#", where '#' represents a null node.
Given a string of comma-separated values preorder, return true if it is a correct preorder traversal serialization of a binary tree.
It is guaranteed that each comma-separated value in the string must be either an integer or a character '#' representing null pointer.
You may assume that the input format is always valid.
- For example, it could never contain two consecutive commas, such as
"1,,3".
Note: You are not allowed to reconstruct the tree.
Examples:
Example 1:
Input: preorder = "9,3,4,#,#,1,#,#,2,#,6,#,#"
Output: true
Example 2:
Input: preorder = "1,#"
Output: false
Example 3:
Input: preorder = "9,#,#,1"
Output: falseSolution in Python
To solve this problem, we need to check whether a given preorder traversal string is a valid serialization of a binary tree. This problem can be approached by simulating the construction of the binary tree as we process the string. Specifically, we track the number of “slots” available for placing child nodes and update this count as we process each node.
Key Ideas:
- Slot System: Each node in a binary tree uses a “slot.” A non-null node (an integer) consumes one slot but generates two new slots (for its left and right children). A null node (
#) simply consumes one slot but does not generate any new slots. - Validation: As we process the nodes in the preorder string, we maintain a count of available slots. If at any point we have no available slots but are still processing nodes, or if there are extra slots left over after all nodes have been processed, then the string does not represent a valid tree.
Plan:
- Start with one slot for the root of the tree.
- Traverse the preorder string:
- If a node is non-null (an integer), it uses one slot and adds two more.
- If a node is null (
#), it uses one slot and does not add any new slots.
- If at any point we use more slots than available, the serialization is invalid.
- After processing all nodes, we should have exactly zero slots remaining for the serialization to be valid.
class Solution:
def isValidSerialization(self, preorder: str) -> bool:
# Split the input string by commas to get the nodes
nodes = preorder.split(',')
# Start with one available slot for the root
slots = 1
# Process each node in the preorder traversal
for node in nodes:
# Each node consumes one slot
slots -= 1
# If at any point we run out of slots, it's invalid
if slots < 0:
return False
# Non-null node (integer): it generates two additional slots
if node != '#':
slots += 2
# After processing all nodes, all slots should be filled (i.e., slots should be 0)
return slots == 0Explanation:
- Splitting the String:
- The input string is split by commas to get individual nodes. Each node can either be a number (indicating a non-null node) or
#(indicating a null node).
- The input string is split by commas to get individual nodes. Each node can either be a number (indicating a non-null node) or
- Slot Counting:
- We start with 1 slot, which is initially reserved for the root of the tree.
- As we process each node:
- If the node is non-null (an integer), it consumes 1 slot but generates 2 new slots (for its left and right children).
- If the node is null (
#), it consumes 1 slot and does not generate any new slots.
- Checking Validity:
- If at any point the number of slots becomes negative, that means there are more nodes than the tree can handle, so the preorder traversal is invalid.
- After processing all nodes, we check whether we have used exactly all the slots (i.e.,
slots == 0). If there are extra slots remaining, the serialization is also invalid.
Solution in C++
class Solution {
public:
bool isValidSerialization(string preorder) {
// Split the input string into nodes using a stringstream and a comma as delimiter
stringstream ss(preorder);
string node;
int slots = 1; // A valid tree starts with one slot for the root
// Process each node in the preorder string
while (getline(ss, node, ',')) {
// For every node we encounter, we consume one slot
slots--;
// If at any point we have negative slots, it's an invalid tree
if (slots < 0) {
return false;
}
// Non-null nodes (i.e., any number) create two additional slots
if (node != "#") {
slots += 2;
}
}
// All slots should be exactly consumed, meaning the tree structure was valid
return slots == 0;
}
};Solution in Javascript
var isValidSerialization = function(preorder) {
// Split the input string by commas to get each node in the traversal.
let nodes = preorder.split(',');
// Initialize the number of available "slots" for nodes.
// A non-null node consumes one slot but creates two new slots (for its two children).
// A null node ('#') consumes one slot without creating new slots.
let slots = 1;
// Traverse each node in the preorder string.
for (let i = 0; i < nodes.length; i++) {
// Decrement the number of available slots as we process the current node.
slots--;
// If at any point we have no available slots but still have more nodes to process, return false.
if (slots < 0) {
return false;
}
// If the current node is not a null node ('#'), it creates two new slots.
if (nodes[i] !== '#') {
slots += 2;
}
}
// After processing all nodes, we should have exactly 0 slots remaining for a valid serialization.
return slots === 0;
};Solution in Java
class Solution {
public boolean isValidSerialization(String preorder) {
// Split the input string by commas to get the preorder tokens
String[] nodes = preorder.split(",");
// We start with 1 slot, which corresponds to the root node
int slots = 1;
// Traverse each node in the preorder traversal
for (String node : nodes) {
// For each node, we need to consume one slot
slots--;
// If at any point we have no slots left to fill, it's invalid
if (slots < 0) {
return false;
}
// If the current node is not a null node (i.e., not "#"),
// it adds two more slots (for its left and right children)
if (!node.equals("#")) {
slots += 2;
}
}
// At the end, all slots should be filled (i.e., slots should be zero)
return slots == 0;
}
}